[DBMS] 정규화 normalization

Published: by Creative Commons Licence

참고 문서

정규화란?

테이블 간의 관계 및 테이블 속성 간의 종속관계 등을 고려하여 중복되는 항목을 삭제하거나 새로운 엔티티를 정의하는 일련의 작업을 정규화(normalization)라고 한다. 정규화는 아래의 여섯 단계로 나뉘며 각 단계를 거친 결과물을 '제 N정규형(normal form)'이라 한다. 참고로 어떤 정규형에도 속하지 않으면 해당 테이블은 그냥 비정규 릴레이션 혹은 비정규 테이블이다. 쉽다

정규화는 1 - 2 - 3 - (필요한경우)BCNF - 4 - 5 순으로 진행되며 각 정규형은 하위 정규형을 반드시 포함한다. 예를 들어 제 3정규형은 제1 정규형과 제 2정규형을 만족한다.

제 1정규형, 1NF

테이블의 모든 속성의 도메인이 원자값으로 구성된 정규형이다.

위의 학생 테이블은 한명의 학생에 다수의 수강과목 데이터가 존재한다. 이 테이블이 제 1정규형을 만족하려면 다음처럼 수강과목 속성이 원자값이 되도록 분리해야 한다.

제 2정규형, 2NF

제 2정규형을 이해하려면 우선 함수적 종속(functional dependency)에 대해 알아야 한다. 테이블 R에서 속성 X의 값 각각에 대해 시간과 관계없이 항상 속성 Y의 값이 오직 하나만 연관되어 있을 때 Y는 X에 함수적 종속이며 X가 Y를 함수적으로 결정한다고 한다. 이를 X->Y로 표기하며 X를 결정자(determinant) Y를 종속자(dependent)라 한다.

쉽게 말해 SELECT문에서 WHERE절의 조건 X에 어떠한 값을 할당해도 출력되는 결과의 수가 항상 하나를 초과하지 않으면 X->Y의 관계가 성립한다고 보면 된다. 이 경우 X는 보통 해당 테이블의 기본키이거나 유일키다.

제 2정규형은 기본키가 아닌 모든 속성이 기본키에 완전 함수적 종속인(혹은 부분 함수적 종속이 없는) 정규형이다. 테이블 R에서 속성 Y가 다른 속성들의 집합 X 전체에 대해 함수적 종속이면서 속성 집합 X의 어떠한 진부분 집합에도 함수적 종속이 아닐 때 Y는 X에 완전 함수적 종속이라 한다.

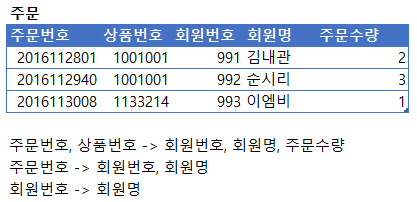
위 주문 테이블에선 총 세 개의 함수적 종속이 존재한다. 회원번호와 회원명, 주문수량은 기본키인 주문번호와 상품번호에 함수적 종속이지만 회원번호와 회원명은 주문번호와 회원번호에도 함수적 종속이다. 기본키에 결정되는 종속자가 기본키의 부분 집합에도 종속될 때 부분 함수적 종속이 발생한다고 하는데, 부분 함수적 종속이 발생할 땐 완전 함수적 종속이 만족되지 않으므로 제 2정규형이 아니다.

따라서 부분 함수적 종속인 회원번호와 회원명을 제거하거나 별도의 테이블로 분리한다.

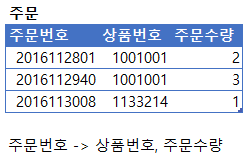
제 3정규형, 3NF

기본키가 아닌 모든 속성이 기본키에 대해 이행적 함수적 종속이 없는 정규형이다. X->Y이고 Y->Z일 때 X->Z를 만족하는 관계를 이행적 함수적 종속이라고 한다. 아래 예를 보자.

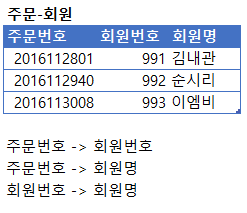
주문번호가 회원번호를 결정하고, 회원번호는 회원명을 결정한다. 여기서 주문번호가 회원명을 결정하기도 하므로 이 테이블은 이행적 함수적 종속이 존재하며 제 3정규형이 아니다. 따라서 아래처럼 분해한다.

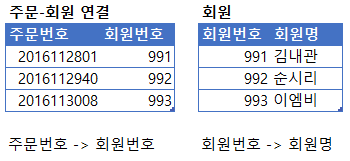
BCNF(Boyce–Codd normal form)

제 3정규형인 테이블 R에서 X->Y 관계인 모든 X와 Y에 대하여 Y가 X의 부분집합이거나 X가 후보키인 정규형이다. 간단하게 말해서 테이블의 모든 결정자가 후보키일 때 BCNF를 만족한다.

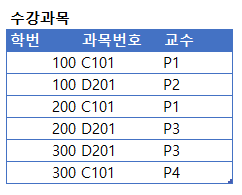
위의 수강과목 테이블에서 PK는 학번과 과목번호다. 학번, 과목번호->교수인 관계이면서 교수->과목번호 관계도 성립한다. 그런데 과목번호는 교수의 부분집합이 아니며 교수는 후보키가 아니기 때문에 BCNF가 아니다. 따라서 다음처럼 분해한다.

제 4정규형, 4NF

테이블에 다중 값 종속(혹은 다치 종속, multi valued dependency) X->>Y가 존재할 경우 테이블의 모든 속성이 X에 함수적 종속인 정규형이다. X, Y, Z 3개의 속성을 가진 테이블에서 복합 속성 X, Z에 대응하는 Y 값의 집합이 X 값에만 종속되고 Z 값에는 무관하면 Y는 X에 다중 값 종속이며 X->>Y로 표기한다.

사실 무슨 소린지 이해를 못해서 예시를 못 만들었다. 😒

제 5정규형, 5NF

테이블의 모든 조인 종속이 후보키를 통해서만 성립되는 정규형이다. 테이블 R의 속성에 대한 부분집합 X, Y, Z가 있다고 할 때 테이블 R이 자신의 프로젝션 X, Y, Z를 모두 조인한 결과와 동일하면 테이블 R은 조인 종속 JD(X, Y, Z)를 만족한다고 한다.

대충 알 것 같은데 귀찮아서 넘어감.

끗.